Functions and graphs.
- Function: a function f:X→Y from one set X to another set Y is an operation which assigns to each element x in X, a single element f(x) in Y.
Very often, f(x) is given by a formula (such as 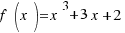 ) which tell us how to compute f(x) when x is given. The process of calculating f(x) is called evaluating f at x. We call x the independent variable.
) which tell us how to compute f(x) when x is given. The process of calculating f(x) is called evaluating f at x. We call x the independent variable.
To visualize a function, we can draw its graph.
- Graph: Let f:X→Y be a function. The set of all points (x,y) in the plane with x in X and y=f(x) is called the graph of f.
We can construct a graph with a determinates data, or we can draw a graph of a function.
Example 1: Soccer tournament.
We do a tournament of Pro with our friends, we put in a graphic the results according to the matchs that each friend win. In the graph, we put in the axis X (the horizontal axis) the names of our friends, and in the axis Y (the vertical axis) the number of the matchs that each friend win. Then, if we see this graph, we quickly will see who friend won more matchs, who friend won least matchs, etc…Now, this is an example of a tournament of Pro:
Graphic 1:
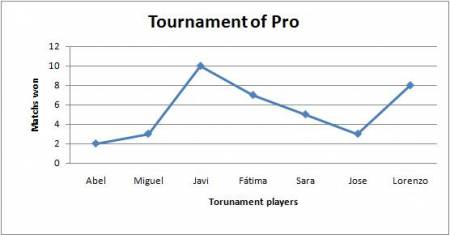
You see the last graph, and you answer the following questions:
- Who did our friends win more matchs?
- Who did our friends win least matchs?
- Who did our friends win four matchs?
- Who did our friends win seven matchs?
But your friends maybe can´t play with you, and you have to play alone. You could do your graph. In this graphic you will put development in your game.
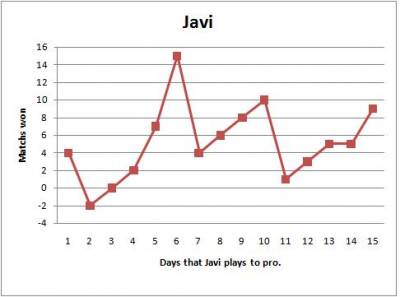
 Javi plays to the Pro every day, he plays ten matchs each day, and he puts his results for 15 days in a graph, like this he will see his development in this graph.
Javi plays to the Pro every day, he plays ten matchs each day, and he puts his results for 15 days in a graph, like this he will see his development in this graph.
Graph 2:
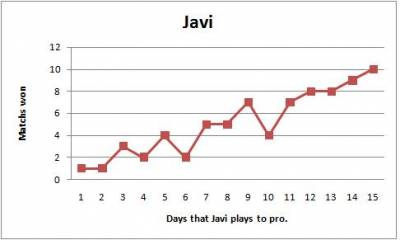
You see the last graph, what could you say of Javi development in the game?
Now, we have the following graph:
Graph 3:
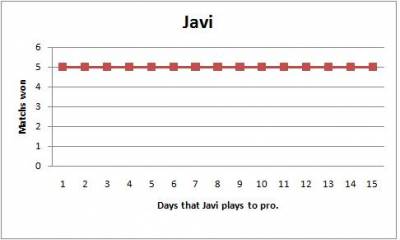
In the graph 3, what could you say of Javi development?
Graph 4:
Do you see any mistake in the graph 4?
Increasing and Decreasing Functions.
Let f be a function defined on an interval I.
- If
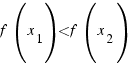 for all
for all 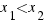 in I, we say that f is increasing on I.
in I, we say that f is increasing on I.
Example 2
The function f(x)=x is increasing on all real-number, because for all  ,
, 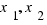 are real-number,
are real-number, 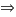
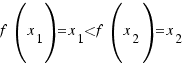 .
.
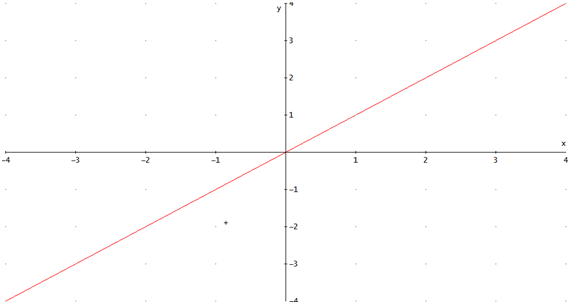
Graph 5:
- If
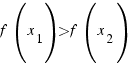 for all
for all 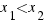 in I, we say that f is decreasing on I.
in I, we say that f is decreasing on I.
Example 3.
The function 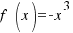 is decreasing in all real-number, because for all
is decreasing in all real-number, because for all 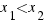 ,
, 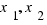 real-number,
real-number, 
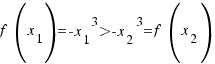 .
.
Graph 6:
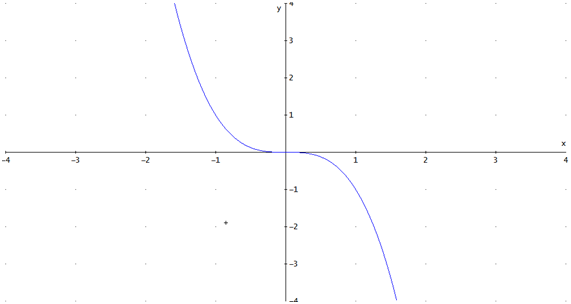
Exercise: Study the graph 2, when is the function increasing and decreasing?How is the development of Javi when the function is increasing or decreasing?
Domain and range.
Let f:X→Y be a function from one set X to another set Y. The set X is called domain of f, and the another set Y is called range of f.
If we specify a function by a formula like 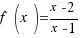 , its domain may be assumed to consist of all x for which the formula is defined (in this case all
, its domain may be assumed to consist of all x for which the formula is defined (in this case all 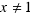 ), unless another domain is explicitly mentioned.
), unless another domain is explicitly mentioned.
Example 4
In the graph 5, the domain and the range are the same, all real-number. In the graph 6 the domain and the range are all real-number.
Exercise: Which are the domain and the range in the graph 2?
Maximum and minimum of a function.
Let f:X→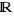 be a function, and let
be a function, and let 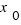 in X.
in X.
- We say that f attains its maximum at
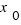 if we have
if we have 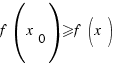 for all x in X. (i.e., the value of f at the point
for all x in X. (i.e., the value of f at the point  is larger than or equal to the value of f at any other point in X).
is larger than or equal to the value of f at any other point in X). - We say that f attains its minimum at
 if we have
if we have 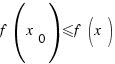 for all x in X. (i.e., the value of f at the point
for all x in X. (i.e., the value of f at the point 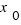 is smaller than equal to the value of f at any other point in X).
is smaller than equal to the value of f at any other point in X).
Example 5
In the graph 5, there isn´t a maximum and minimum, because the function is increasing for all real-number, and f never attains a maximum or minimum.
Exercise: Calculate the minimum and the maximum in the graphs one and two. Describe the relation between the maximum (minimum) and the matchs played.
Other exercise: In the following page: www.lpf.es, you can see all the information of the spanish tournament soccer. You can construct a graph with these data, you put in the axis X all teams of soccer, and in the axis Y the position of each team in the tournament.





