When we want to determine the position of a point in the plane, we use a some axes on a squared pattern. Then, to determine a point on the lunar surface we use a similar system, only that in this case, the straight lines are replaced with meridians and parallels.
The system of geographical coordinates is determined of this way:
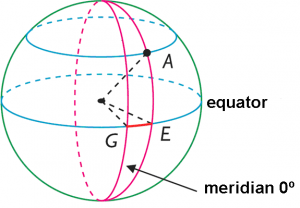
* The axes : there takes as a horizontal axis the equator (it passes for the crater Manilio) and as vertical axis the meridian 0º (it passes for the crater Mösting A).
* The origin of coordinates is the point of intersection of the equator with the meridian 0º
* The magnitude is degree.
To determinate the geographical coordinates of a point on the lunar surface, we must know the
LENGTH and the LATITUDE of this point.
—GEOGRAPHICAL LENGTH: It is the arch GE on the equator measured in degrees from the meridian 0º up to the meridian that passes for the point A. Therefore, the length of a place is measured of 0º to 180º easter direction and of 0º to 180º direction west .
—GEOGRAPHICAL LATITUDE: It is the arch EA on the meridian of the point A measured in degrees from the equator to the mentioned point. Therefore, the latitude of a place is measured of 0º to 90º in north direction and of 0º to 90º in south direction.
![]() How do I calculate the distance of two points that are in same parallel?
How do I calculate the distance of two points that are in same parallel?
== Example ==
<html>
<span style=“color:purple;font-size:120%;”>
A village A and a village B are placed in a parallel which latitude is of 50º north in the terrestrial globe.<br>
The length of the village A is 10º west and the length the village B is 25º east.<br>
<br>
What is the distance that is between A y B?</span>
</html>
Let's bear in mind that the villages are in the terrestrial surface and the radius of the Earth is R = 6370km
First, we calculate the radius of the circumference that is formed in the parallel one of latitude 50º.Observes the following figure:

<m15>{cos50º = r/6370}</m><m 20>doubleright</m><m15>{r= cos50º*6370=4094km}</m>
Now, we calculate the length of arch that both points determine: 10º + 25º = 35º
<m15>{L={2.Pi.r.nº}/{360º}={2.Pi.4094.35º}/{360º}=2501 km}</m>
The distance between the village A and B is 2501 km.![]()




