Tabla de Contenidos
Measure the height of a mountain in the illuminate zone of the moon.
What do you need?
- Paper and pen.
- The program Salsa J (you can download this program in this page. http://www.houspain.com/gttp/salsaj) for the image proccesing.
- Knowledge of:
Exercise.
Estimate the height of a mountain of the moon.
Working out.
What do we Know?
In this exercise we only Know the diameter of the moon, 3476 Km. The other dates that we´ll need for we solve the exercise, we will find out by using the program SalsaJ for the image processing.
What do we have to find out?
The objective of this exercise is to Know the height of the mountains of the moon by using mathematics.
Work out
You will can solve this exercise if you do the following points:
- With the program SalsaJ open the photo of the previus point.
- En the photo, the blue circles show the mountains that you can study.
- We have to write the scale of the photo in the program SalsaJ, for this we only need to Know the diameter of the moon.
- What is the distance between the terminador and the mountain shadow (the segment CA)?. Terminador is the line that differentiate the illuminate zone of the not illuminate zone of the moon.
- We know the radius of the moon, because we know the diameter of the moon: 3476 Km.
- Determinate the length of the mountain shadow (the segment AB) using the SalsaJ program.
- Identificate, in the figure of the point 11, two rights triangles.
- In each right triangle of the previus point, apply the Pythagorean theorem.
- Rename the segments with letters (you look the next point).
- Calculate the height of the mountain with a second degree equation. For your need, look the next figure:
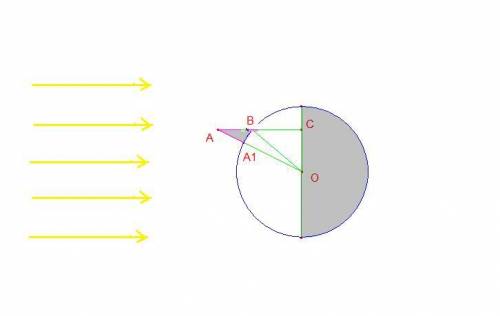
AB = s (length of the moon shadow)
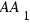 = a (mountain height)
= a (mountain height)
BC = d (distance of the mountain to the mountain)
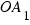 = OB = R (radius of the moon)
= OB = R (radius of the moon)
B = the tip of the shadow of the mountain.
NOTE: The solution will be in function of R, d and s.






