Tabla de Contenidos
Thales' theorem
First idea
Let's try to deduce what Thales of Miletus found out long time ago.Play with the next dynamic worksheet.
If some dynamic worksheets are not available, java can be download from the page:
Move D and E.
- Is there any relationship between the straight lines
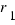and 
? And 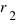between 
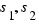and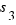 
?
- Watch the results when we divide a/b and c/d. What do you observe?
- Do you come to a conclusion?
- Move D and E again,what happens?
- Do you think it would always occur the same fact?
- What would happen if the straight lines 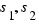and 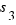weren't parallel?
Observe the next dynamic worksheet.
Is there any relationship with the the dynamic worksheet above?
Formally
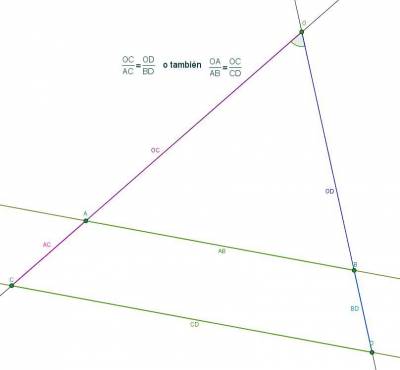
THALES' THEOREM:
“When paralell stright lines cut two secant right lines, the ratios of any 2 segments on the first line equals the ratios of the according segments on the second line”.
On the picture, a/c = b/d.
THALES' TRIANGLES:
Two triangles are Thales' triangles when they fulfill the next two properties:
- They have an angle in common
- The opposite sides to this angle are paralell.
Exercises
You can use similar Thales' theory to do the next exercise:
